Page 129 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 129

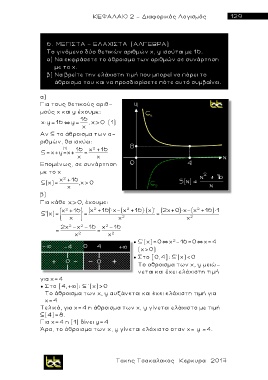
6. ΜΕΓΙΣΤΑ – ΕΛΑΧΙΣΤΑ (ΑΛΓΕΒΡΑ)
Το γινόμενο δύο θετικών αριθμών x, y ισ ο ύται με 16.
α) Να εκφράσετε το άθροισμα των αριθμών σε συνάρτηση
με το χ.

β) Να βρείτε την ελάχιστη τιμή που μπορεί να πάρει το
άθροισμα του και να προσδιορίσετε πότε αυτό συμβαίνει.

α )
Για τους θετικούς αριθ-
μούς x και y έχουμε:
16
x× y 16 y , x 0 (1)
x
Αν S το άθροισμα των α-
ριθμών, θα ισχύει:
2
(1 ) 16 x +16
S= x+y =x+ =
x x
Επομέν ω ς, σε συνάρτηση

με το χ
x +16
2
S(x)= , x> 0
x
β )
Για κάθε x 0, έχουμε:
x +16 (x +16)'× x-(x +16)×(x)' (2x+0 )× x-(x +16)× 1
2
2
2
2
S'(x)= ' = =
x x 2 x 2

2
2x -x -16 x -16
2
2
= =
x 2 x 2
● S'(χ)=0`χ -16=0`χ=4
2
(χ>0)
● Στο [0,4]: S'(χ)<0
Τ ο αθροισμα των x, y μειώ-
νεται και έχει ε λ άχιστη τιμή
για χ=4
● Στο [4,+þ): S '(χ)>0
Τ ο άθροισμα των x, y αυξάνεται και έχει ελάχιστη τιμή για
χ = 4
Τελικά, για χ=4 η άθροισμα των x, y γίνεται ελάχιστο με τιμή
S(4)=8.
Για χ=4 η (1) δίνει y=4
Άρα, το άθροισμα των x, y γίνεται ελάχιστο οταν x= y =4.

Τακης Τσακαλακος Κερκυρα 2017