Page 131 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 131

ΠΑΡΑΔΕΙΓΜΑΤΑ

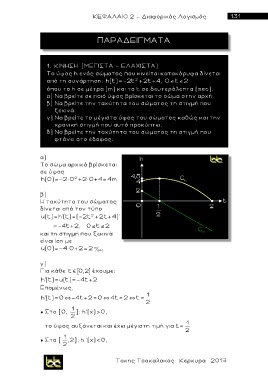
1. ΚΙΝΗΣΗ (ΜΕΓΙΣΤΑ – ΕΛΑΧΙΣΤΑ)
Το ύψος h ενός σώματος που κινείται κατακόρυφα δίνεται
α π ό τη συνάρτηση: h(t)=-2t +2t+4, 0 t 2
2
όπου το h σε μέτρα (m) και το t σε δευτερόλεπτα (sec).
α) Να βρείτε σε ποιό ύψος βρίσκεται το σώμα στην αρχή.
β) Να βρείτε την ταχύτητα του σώματος τη στιγμή που
ξεκινά.
γ) Να βρείτε το μέγιστο ύψος του σώματος καθώς και την
χρονική στιγμή που αυτό προκύπτει.
δ) Να βρείτε την ταχύτητα του σώματος τη στιγμή που
φ τ άνει στο έδαφος.

α )
Το σώμα αρχικά βρίσκεται

σε ύψος

2
h(0)=-2× 0 +2× 0+4 =4 m

β )

Η ταχύτητα του σώματος
δίνεται από τον τύπο

u(t)=h'(t)=(-2t +2t+4)'
2

-4t+2, 0 t 2

και τη στιγμή που ξεκινά
είναι ίση με

u(0)=-4× 0+2=2 m sec

γ )

Για κάθε t 0,2 έχουμε:

h'(t)=u(t)=-4t+2

Επομένως,

h'(t)= 0 -4t+2= 0 4t= 2 t= 1
2
1
● Στο [0, ]: h'(χ)>0,
2
το ύψος αυξάνεται και έχ ε ι μέγιστη τιμή για t= 1
2
1
● Στο [ ,2]: h '(χ)<0,

2

Τακης Τσακαλακος Κερκυρα 2017