Page 134 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 134

3. ΦΥΣΙΚΗ (ΜΕΓΙΣΤΑ – ΕΛΑΧΙΣΤΑ)
Η ενέρ γ εια w(t), που αποδίδεται από ένα πηνίο, μεταβάλ-
λεται με το χρόνο t σύμφωνα με τον τύπο της συνάρτησης
w t 6t 2 t , και μετριέται σε joules.
4

α) Να εκφράσετε το ρυθμό μεταβολής της ενέργειας ως
προς το χρόνο (την ισχύ του πηνίου P) τη χρονική στιγ-
μή t t ,
0
β ) Σε ποιά χρονική στιγμή το πηνίο έχει μέγιστη ισχύ;
γ) Πόσα Watt είναι η μέγιστη ισχύς του πηνίου;

α )
Είναι για t > 0

w'(t)= p(t)=(6t -t )'
4
2

= 12t-4t 3

και ο ρυθμός μεταβολής

της ενέργειας ως προς το
χ ρ όνο (η ισχύς του πηνίου

P) τη χρονική στιγμή t t ,
0

είναι
P(t ) w'(t ) 12t 0 4t
3

0
0
0
β )

Για κάθε t 0, έχουμε:

3
2
Ρ'(t)=(12t-4t )' =12-12t
t 0
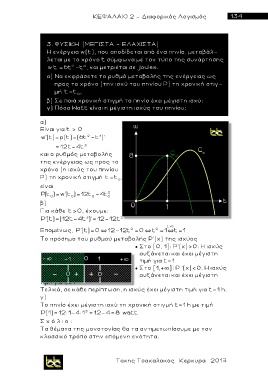
Επομένως, Ρ'(t)=0 12 12t 2 0 t 2 1 t 1

Το πρόσημο του ρυθμού μεταβολής Ρ'(χ) της ισχύο ς
● Στο [0, 1]: Ρ'(χ)>0. Η ισχύς

αυξάνεται και έχει μέγιστη

τιμή για t=1
● Στο [1,+ þ ]: Ρ '(χ)<0. Η ισχύς

αυξάνεται και έχει μέγιστη

τιμή για t=1
Τελικά, σε κάθε περίπτωση, η ισχύς έχει μέγιστη τιμή για t=1 h.

γ )

Το πηνίο έχει μέγιστη ισχύ τη χρονική στιγμή t=1 h με τιμή
3
Ρ(1)=12× 1-4× 1 =12-4=8 watt

Σ χ ό λ ι ο :

Τα θέματα της μονοτονίας θα τα αντιμετωπίσουμε με τον

κλασσικό τ ρ όπο στην επόμενη ενότητα.

Τακης Τσακαλακος Κερκυρα 2017