Page 138 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 138

ΠΑΡΑΔΕΙΓΜΑΤΑ

1. ΣΧΕΣΗ ΡΥΘΜΩΝ ΜΕΤΑΒΟΛΗΣ
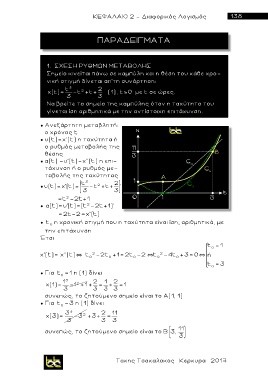
Σημείο κινείται πάνω σε καμπύλη και η θέση του κάθε χρο-
νική στιγμή δίνεται απ'τη συνάρτηση:
t 3 2
2
χ(t)= 3 -t +t+ 3 (1), t 0 με t σε ώρες.

Να βρείτε τα σημεία της καμπύλης όταν η ταχύτητα του
γίνεται ίση αριθμητικά με την αντίστοιχη επιτάχυνση.

● Ανεξάρτητη μεταβλητή:

ο χρόνος t
● υ ( t)=x'(t) η ταχύτητα ή

ο ρυθμός μεταβολής της

θέσης
● α ( t) =υ'(t)=x''(t) η επι-

τάχ υ νση ή ο ρυθμός μ ε -

ταβολής της ταχύτητας

● υ(t)= x'(t)= t 3 -t +t+ 2 '
2
3
3

t -2t+1
2

● α(t)=υ'(t)=(t -2t+1)'
2
=2t- 2 x''(t )

● t η χρονική στιγμή που η ταχύτητα είναι ίση, αριθμητικά, με
0
την επιτάχυνση
Έτσι

t = 1
0
x'(t)= x''(t)` t 2 -2t +1= 2t 2 `t 2 -4t +3= 0` ή
0 0 0 0 0
t = 3
0

● Για t = 1 η (1) δίνει
0
1 3 2 1 2
x(1)= -1 +1 + + 1
2
3 3 3 3
συνεπώς, το ζητούμενο σημείο είναι το Α(1, 1)

● Για t =3 η (1) δίνει
0

x(3)= 3 3 -3 2 +3+ 2 11
3
3
3

συνεπώς, το ζητούμενο σημείο είναι το Β 3, 11
3

Τακης Τσακαλακος Κερκυρα 2017