Page 140 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 140

3. ΕΦΑΠΤΟΜΕΝΗ (ΓΩΝΙΑ)
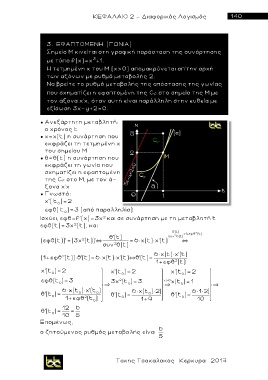
Σημείο Μ κινείται στη γραφική παράσταση της συνάρτησης
με τύπο f(x)=x +1.
3

H τετμημένη χ του Μ (χ>0) απομακρύνεται απ'την αρχή
των αξόνων με ρυθμό μεταβολής 2.
Να βρείτε το ρυθμό μεταβολής της απόστασης της γωνίας
που σχηματίζει η εφαπτομένη της C f στο σημείο της Μ με
τον άξονα χ'χ, όταν αυτή είναι παράλληλη στην ευθεία με
εξίσωση 3χ-y+2=0.

● Ανεξάρτητη μεταβλητή:
ο χρόνος t
● χ = x(t) η συνάρτηση που
εκφράζει τη τετμημένη χ
του σημείου Μ
● θ=θ(t) η συνάρτηση που
εκφράζει τη γωνία που
σχηματίζει η εφαπτομένη
της C f στο Μ, με τον ά-
ξονα χ'χ
● Γνωστά:
χ'( t )=2
0
εφθ( t )=3 (από παραλληλία )
0
Ισχύει, εφθ=f'(x)=3x 2 και σε συνάρτηση με τη μεταβλητή t
2
εφθ(t)=3x (t), και
θ'(t) =1 εφθ (t)
2
θ'(t) συν θ(t)
2
(εφθ(t))' =(3x (t))'` = 6 × x(t)× x'(t) `
2
συν θ(t)
2
6 × x(t)× x'(t)
2
(1+εφθ (t))× θ'(t)= 6 × x(t)× x'(t) `θ'(t)=
1+εφθ (t)
2
x'(t ) 2 x'(t ) 2 x'(t ) 2
0
0
0
εφθ(t )= 3 3χ (t )= 3 χ > 0 χ(t )= 1 ~
2
0
0
0
6 × x(t )× x'(t ) 6 × x(t )× 2 ) 6 × 1× 2 )
θ'(t )= 0 0 θ'(t )= 0 θ'(t )=
0 1+εφθ (t ) 0 1+9 0 10
2
0
12 6
θ'(t )= 10 = 5
0
Επομένως,
6
ο ζητούμενος ρυθμός μεταβολής είναι
5

Τακης Τσακαλακος Κερκυρα 2017