Page 141 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 141

4. ΟΙΚΟΝΟΜΙΑ (ΧΡΟΝΙΚΟΣ ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ)
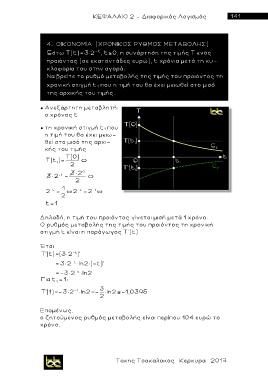
Έστω Τ(t)=3×2 -t , t 0, η συνάρτηση της τιμής Τ ενός
προιόντος (σε εκατοντάδες ευρώ), t χρόνια μετά τη κυ-

κλοφορία του στην αγορά.
Να βρείτε το ρυθμό μεταβολής της τιμής του προιόντος τη
χρονική στιγμή t 1 που η τιμή του θα έχει μειωθεί στο μισό
της αρχικής του τιμής.

● Ανεξάρτητη μεταβλητή:
ο χρόνος t

● τη χρονική στιγμή t 1 που
η τιμή του θα έχει μειω-
θ ε ί στο μισό της αρχι-
κής του τιμής
T(0)
T(t )= 2 `
1

3 × 2 0
3 × 2 -t `
2
1
2 -t ` 2 -t 2 `
-1
2
t 1

Δηλαδή, η τιμή του προιόντος γίνεται μισή μετά 1 χρόνο.
Ο ρυθμός μεταβολής της τιμής του προιόντος τη χρονική
στιγμή t είναι η παράγωγος T'(t)

Έτσι
T'(t)= (3× 2 )'
-t
= 3× 2 -t × ln2×(-t)'

=-3× 2 -t × ln2
Για t = 1:
1

T'(1)= -3× 2 -1 × ln2= - 3 × ln2 -1,0395
2

Επομένως,
ο ζητούμενος ρυθμός μεταβολής είναι περίπου 104 ευρώ το
χ ρ όν ο .

Τακης Τσακαλακος Κερκυρα 2017