Page 149 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 149

Θ Ε Ω Ρ Ι Α ...

Θ ε ώ ρ η μ α R o l l e
Αν για μία συνάρτηση f ισχύουν:
● Είναι σ υ ν ε χ ή ς στο κλειστό διάστημα [α, β].
● Είναι π α ρ α γ ω γ ί σ ι μ η στο ανοικτό διάστημα (α, β).
● f ( α ) = f ( β )
Τότε υπάρχει έ ν α τ ο υ λ ά χ ι σ τ ο ν ξ που ανήκει στο
(α, β) τέτοιο ώστε f ' ( ξ ) = 0

δηλαδή υ π άρχει μία τουλάχιστον ρίζα της παραγώγου στο
διάστημα (α,β).

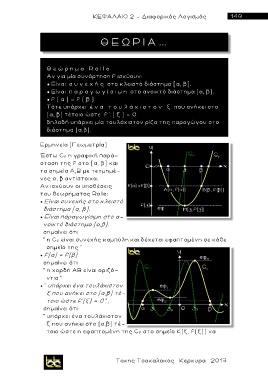
Ερμηνεία (Γ ε ωμετρία )

Έστω C f η γραφική παρά-
σταση της f στο [α, β] και

τα σημεία Α,Β με τετμημέ-

νες α, β αντίστοιχα.

Αν ισχύουν οι υποθέσεις
του θεω ρ ήματος Rolle:

 Είναι συνεχής στο κλειστό

διάστημα [α, β].
 Είναι πάραγωγίσιμη στο α-

νοικτό διάστημα (α,β).

σημαίνει ότι

" η C f είναι συνεχής καμπύλη και δέ χ εται εφαπτομένη σε κάθε
σημείο της "

 f(α) = f(β)

σημαίνει ότι
" η χορδή ΑΒ είναι οριζό-

ντια "

 “ υπάρχει ένα τουλάχιστον

ξ που ανήκει στο (α,β) τέ-
τοιο ώστε f'(ξ) = 0 ”,

σημαίνει ότι

“ υπάρχει ένα τουλάχιστον
ξ που ανήκει στο (α,β) τέ-

τοιο ώστε η εφαπτομέν η της C f στο σημείο Κ(ξ, f(ξ)) να

Τακης Τσακαλακος Κερκυρα 2017