Page 150 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 150

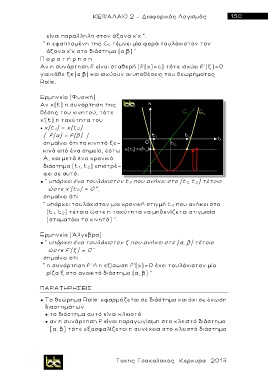
είναι παράλληλη στον άξονα x’x “.
“ η εφαπτομένη της C f τέμνει μία φορά τουλάχιστον τον
άξονα x’x στο διάστημα (α,β) “
Π α ρ α τ ή ρ η σ η

Αν η συνάρτηση f είναι σταθερή (f(x)=c) τότε ισχύει f'(ξ)=0
για κάθε ξ (α,β) και ισχύουν οι υποθέσεις του θεωρήματος
Rolle.

Ερμηνεία (Φυσική)
Αν χ(t) η συνάρτηση της
θέσης του κινητο ύ , τότε

χ'(t) η ταχύτητα του
 χ(t 1) = χ(t 2)
( f(α) = f(β) )

σημαίνει ότι το κινητό ξ ε -
κινά α π ό ένα σημείο, έστω
Α, και μετά ένα χρονικό
διάστημα (t 1, t 2) επιστρέ-
φει σε αυτό.
● “ υπάρχει ένα τουλάχιστον t 0 που aνήκει στο (t 1, t 2) τέτοιο
ώστε x'(t 0) = 0 ”,

σημαίνει ότι
“ υπάρχει τουλάχιστον μια χρονική στιγμή t 0 που ανήκει στο
(t 1, t 2) τέτοια ώστε η ταχύτητα να μηδενίζεται στιγμιαία
(σταματάει το κινητό) “.

Ερμηνεία (Άλγεβρα)
● “ υπάρχει ένα τουλάχιστον ξ που ανήκει στο (α, β) τέτοιο
ώστε f'(ξ) = 0 ”
σημαίνει oτι
“ η συνάρτηση f' ή η εξίσωση f'(x)=0 έχει τουλάχιστον μία

ρίζα ξ στο ανοικτό διάστημα (α, β ) "

ΠΑΡΑΤΗΡΗΣΕΙΣ

● To θεώρημα Rolle εφαρμόζεται σε διάστημα και όχι σε ένωση
δ ι αστημάτων
● το διάστημα αυτό είναι κλειστό
● αν η συνάρτηση f είναι παραγωγίσιμη στο κλειστό διάστημα
[α, β] τότε εξασφαλίζεται η συνέχεια στο κλειστό διάστημα

Τακης Τσακαλακος Κερκυρα 2017