Page 182 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 182

5. ROLLE – ΑΠΟΔΕΙΞΗ ΑΚΡΙΒΩΣ ΔΥΟ ΡΙΖΕΣ
Αν η συνάρτηση f είναι δύο φορές παραγωγίσιμη στο διά -
στημα Α και ισχύει f''(x) 0 για κάθε χ Α, να αποδείξετε ότι
η εξίσωση 5 -4χ-1=0 έχει ακριβώς δύο ρίζες που ανή-
Χ
κουν στο διάστημα Α.

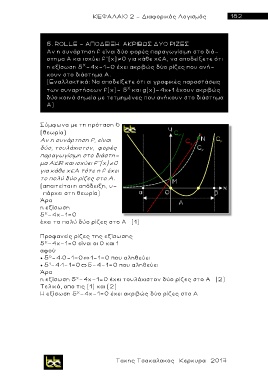
(Εναλλακτικά: Να αποδείξετε ότι οι γραφικές παραστάσεις
των συναρτήσεων f(x)= 5 και g(x)=4x+1 έχουν ακριβώς
Χ
δύο κοινά σημεία με τετμημένες που ανήκουν στο διάστημα
Α )

Σύμφωνα με τη πρόταση 6
(θεωρία )
Αν η συνάρτηση f, είναι
δύο, τουλάχιστον, φορές
παρ α γωγίσιμη στο διάστη-
μα Α και ισχύει f''(χ) 0
για κάθε χ Α τότε η f έχει
το πολύ δύο ρίζες στο Α.
(απαιτείται η απόδειξη, υ-
πάρχει στη θεωρία )
Άρα
η εξίσωση
5 -4 χ -1=0
Χ
έχει το πολύ δύο ρίζες στο Α (1)

Προφανείς ρίζες της εξίσωσης
5 -4 χ -1=0 είναι οι 0 και 1
Χ
αφού
 5 -4×0-1=0`1-1=0 που αληθεύει
0
 5 -4×1-1=0`5-4-1=0 που αληθεύε ι
1
Άρα
η εξίσωση 5 -4 χ -1=0 έχει τουλάχιστον δύο ρίζες στο Α (2)
Χ
Τελικά, απο τις (1) και (2)
Η εξίσωση 5 -4χ-1=0 έχει ακριβώς δύο ρίζες στο Α
Χ

Τακης Τσακαλακος Κερκυρα 2017