Page 186 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 186

2. Θ.Μ.Τ. – ΑΠΟΔΕΙΞΗ ΥΠΟΘΕΣΕΩΝ ΣΧΕΣΗΣ
Δίνεται η συνάρτηση f(x)=x×e . Nα αποδείξετε ότι υπάρχει
X
α ) ξ (0, 1) τέτοιο ώστε: f'(ξ)=e
1
β) κ (-1, 0) τέτοιο ώστε: e κ+1 = κ+1

Έχουμε
f(0)=0 × e = 0
0
f(-1)=(-1) × e -1 =- 1
e
f(1)=1 × e = e
1
f'(χ)=( χ)'e +χ(e )'
χ
χ
e χe
α)
● Η f είναι συνεχής στο δι-
άστημα [0, 1]
(γινόμενο συνεχών)
● Η f είναι παραγωγίσιμη
στο διάστημα (0, 1) (γινόμενο παραγωγίσιμων)
συνεπώς, ισχύουν οι υποθέσεις του Θ.Μ.Τ. στο (0, 1), οπότε
f(1)-f(0) e-0
υπάρχει ξ (0, 1): f'(ξ)= = ` f'(ξ)= e
1-0 1
β )
● Η f είναι συνεχής στο διάστημα [-1, 0] (γινόμενο συνεχών)
● Η f είναι παραγωγίσιμη στο διάστημα (-1, 0) (γινόμενο παρα-
γωγίσιμων)
συνεπώς, ισχύουν οι υποθέσεις του Θ.Μ.Τ. στο (0, 1), οπότε

υπάρχει κ (-1, 0):

0- - 1
f(0)-f(-1) e 1 1
f'(κ)= = ` f'(κ)= ` e κe
0-(-1) 1 e e
1 1
` (κ+1)× e ` e κ+1 =
e κ + 1
Σ χ ό λ ι ο

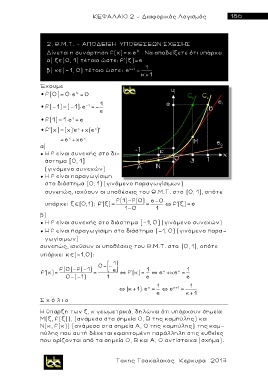
Η ύπαρξη των ξ, κ γεωμετρικά, δηλώνει ότι υπάρχουν σημεία
Μ(ξ, f(ξ)), (ανάμεσα στα σημεία Ο, Β της καμπύλης) και
Ν(κ, f(κ)) (ανάμεσα στα σημεία Α, Ο της καμπύλης) της καμ-
πύλης που αυτή δέχεται εφαπτομένη παράλληλη στις ευθείες
που ορίζονται από τα σημεία Ο, Β και Α, Ο αντίστοιχα (σχήμα).

Τακης Τσακαλακος Κερκυρα 2017