Page 189 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 189

4. Θ.Μ.Τ. – ΑΠΟΔΕΙΞΗ ΥΠΟΘΕΣΕΩΝ (ΠΑΡΑΜΕΤΡΟΣ)
χ +α , χ 1
2
Δίνεται η συνάρτηση f(x)= 3
χ -αχ+β , χ> 1
για την οποία ισχύει το Θ.Μ.Τ. στο διάστημα [ -1, 2].
α) Nα βρείτε τις τιμές των α και β
β) Να αποδείξετε ότι υπάρχει σημείο Μ(ξ, f(ξ)) με ξ (0, 2)
στο οποίο η εφαπτομένη είναι παράλληλη στην ευθεία
ε: 7x-3y+3=0

α )
Αφού ισχύει το Θ.Μ.Τ.

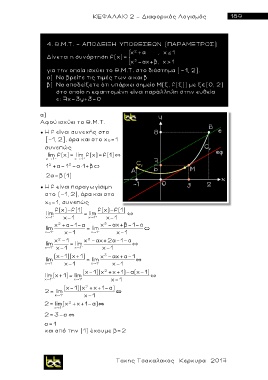
● Η f είναι συνεχής στο
[-1, 2], άρα και στο χ 0=1
συνεπώς
lim f(x)= lim f(x)= f(1)`
x 1 x 1 +
3
2
1 +α= 1 -α× 1+β`
2α= β (1)

● Η f είναι παραγωγίσιμη
στο (-1, 2), άρα και στο
χ 0=1, συνεπώς

lim f(x)-f(1) = lim f(x)-f(1) `
x 1 x-1 x 1 x-1
2
3
lim x +α-1-α = lim x -αχ+β-1 `
x 1 x-1 x 1 x 1
3
2
lim x -1 = lim x -αχ+2α-1 `
x 1 x 1 x 1 x 1
(x-1)(χ+1) x -αχ+α-1
3
lim = lim `
x 1 x-1 x 1 x 1
(x-1)(χ +χ+1)-α(χ-1)
2
lim(χ+1)= lim `
x 1 x 1 x-1
2
2= lim (x-1)(χ +χ+1-α) `
x 1 x-1
2= lim(χ +χ+1-α) `
2
x 1
2= 3-α `

α= 1
και από την (1) έχουμε β=2

Τακης Τσακαλακος Κερκυρα 2017