Page 192 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 192

ΠΑΡΑΔΕΙΓΜΑΤΑ

1. Θ.Μ.Τ. – ΥΠΑΡΞΗ ξ (α, β) ΩΣΤΕ f''(x) = v
Έστω η συνάρτηση f με f(x)=ημx-συνx .
Nα αποδείξετε ότι υπάρχει
π 4
● ξ 1 0, 2 τέτοιο, ώστε f'(ξ)=
π
● ξ 2 2 , π τέτοιο, ώστε f'(ξ)=0
2
● ξ (0, π) τέτοιο, ώστε f''(ξ)= .

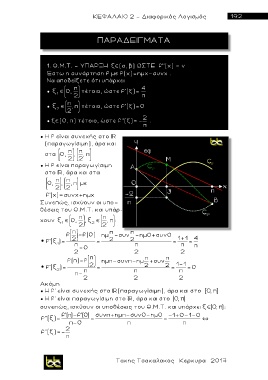
● Η f είναι συνεχής στο
(παραγωγίσιμη), άρα και
π π
στα 0, , , π
2 2
● Η f είναι παραγωγίσιμη
στο , άρα και στα
π π
0, , , π με
2 2
f'(x)=συνχ+ημχ
Συνεπώς, ισχύουν οι υπο-
θέσεις του Θ.Μ.Τ. και υπάρ-
π
π
χουν ξ 1 0, 2 , ξ 2 2 , π :
π π π
f -f(0) ημ -συν -ημ0+συν0
f'(ξ )= 2 = 2 2 = 1+1 = 4
1 π -0 π π π
2 2 2
f(π)-f π ημπ-συνπ-ημ π +συν π
f'(ξ )= 2 = 2 2 = 1-1 = 0
2
π- π π π
2 2 2
Ακόμη
● Η f' είναι συνεχής στο (παραγωγίσιμη), άρα και στο [0, ]
● Η f' είναι παραγωγίσιμη στο , άρα και στο (0 , )
συνεπώς, ισχύουν οι υποθέσεις του Θ.Μ.Τ. και υπάρχει ξ ( 0 , ):
f'( )-f'(0) συνπ+ημπ-συν0-ημ0 -1+0-1-0
f'' (ξ )= = = `
-0 π π

f'' (ξ )=- 2
π

Τακης Τσακαλακος Κερκυρα 2017