Page 196 - diaforikos
P. 196
ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 196
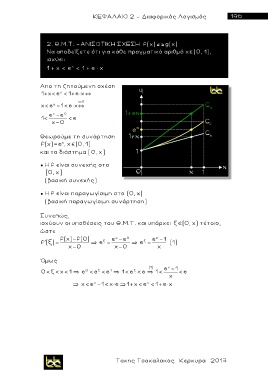
2. Θ.Μ.Τ. –ΑΝΙΣΟΤΙΚΗ ΣΧΕΣΗ f(x)º g(x)
Να αποδείξετε ότι για κάθε πραγματικό αριθμό χ (0, 1),
ισχύει:
1 + χ < e < 1 + e × x
χ
Απο τη ζητούμενη σχέση
1 + χ < e < 1 +e× x`
χ
χ>0
χ < e -1< e× x`
χ
χ
e -e 0
1 < < e
x-0
Θεωρούμε τη συνάρτηση
f(x)=e , x (0, 1)
χ
και το διάστημα [0, χ]
● Η f είναι συνεχής στο
[0, χ]
(βασική συνεχής)
● Η f είναι παραγωγίσιμη στο (0, χ)
(βασική παραγωγίσιμη συνάρτηση)
Συνεπώς,
ισχύουν οι υποθέσεις του Θ.Μ.Τ. και υπάρχει ξ (0, χ) τέτοιο,
ώστε
χ
χ
f'(ξ )= f(x)-f(0) e = e -e 0 e = e -1 (1)
ξ
ξ
x-0 x-0 x
Όμως
χ
(1) e -1
0
ξ
ξ
0<ξ<χ<1 e <e <e 1 1<e <e 1< <e
x
χ<e -1<x× e 1+x< e < 1+e ×x
χ
x
Τακης Τσακαλακος Κερκυρα 2017