Page 184 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 184

ΠΑΡΑΔΕΙΓΜΑΤΑ

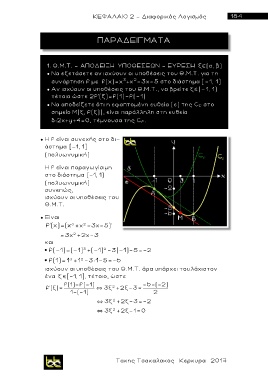
1. Θ.Μ.Τ. – ΑΠΟΔΕΙΞΗ ΥΠΟΘΕΣΕΩΝ – ΕΥΡΕΣΗ ξ (α, β)
● Να εξετάσετε αν ισχύουν οι υποθέσεις του Θ.Μ.Τ. για τ η
συνάρτηση f μ ε f(x)=x +x -3x-5 στο διάστημα [-1, 1]
3
2
● Αν ισχύουν οι υποθέσεις του Θ.Μ.Τ., να βρείτε ξ (-1, 1)
τέτοιο ώστε 2f'( ξ ) =f(1)-f(-1)

● Nα αποδείξετε ότι η εφαπτομένη ευθεία ( ε) της C f στο
σημείο Μ(ξ, f(ξ)), είναι παράλληλη στη ευθεία
δ:2χ+y+4=0, τέμνουσα της C f .

● Η f είναι συνεχής στο δι-
άστημα [-1, 1]
(πολυωνυμική)

Η f είναι παραγωγίσιμη

στο διάστημα (-1, 1)
(πολυωνυμική)
συνεπώς,
ισχύουν οι υποθέσεις του
Θ.Μ.Τ.

● Είναι
f'(x)=(x 3 +x -3x-5)'
2

=3x +2x-3
2
και
f(-1)=(-1) 3 +(-1) 2 -3(-1) -5=-2

1
f(1)=1 3 +1 2 -3× -5=-6
ισχύουν οι υποθέσεις του Θ.Μ.Τ. άρα υπάρχει τουλάχιστον
ένα ξ [-1, 1], τέτοιο, ώστε
f(1)-f(-1) -6-(-2)
f'(ξ)= ` 3ξ +2ξ-3=
2
1-(-1) 2
2
` 3ξ +2ξ-3=-2
` 3ξ +2ξ-1= 0
2

Τακης Τσακαλακος Κερκυρα 2017