Page 220 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 220

ΠΟΡΙΣΜΑ
Αν για δύο συναρτήσεις f, g ορισμένες σε ένα διάστημα Δ
ισχύουν:

 είναι σ υ ν ε χ ε ί ς στο διάστημα Δ.
 για κάθε εσωτερικό σημείο x του Δ ισχύει f ’ ( x ) = g ’ ( x )
τότε, υπάρχει σταθερά c, τέτοια ώστε για κάθε x στο διά-
στημα Δ να ισχύει:
f ( x ) = g ( x ) + c .

ΑΠΟΔΕΙΞΗ

Η συνάρτηση f - g είναι συν-

εχής στο Δ και για κάθε εσω-

τερικό σημείο x∈Δ ισχύει

(f - g)’(x) = f’ ( x) - g’ ( x) = 0
Επομένως,

σύμφωνα με το θεώρημα:

“ Εστω μια συνάρτηση f ορι-
σμένη σε ένα διάστημα Δ.

Αν

 η f είναι σ υ ν ε χ ή ς στο

δ ι άστημα Δ και
 f’ ( x) = 0 για κάθε ε σ ω τ ε ρ ι κ ό σημειο x του Δ, τότε η f

είναι σ τ α θ ε ρ ή σε όλο το διάστημα Δ.”

η συνάρτηση f - g είναι σταθερή στο Δ.
Άρα, υπάρχει σταθερά c τέτοια, ώστε για κάθε x∈Δ να ισχύει

f(x)-g(x)=c, οπότ ε , f(x) = g(x) + c .

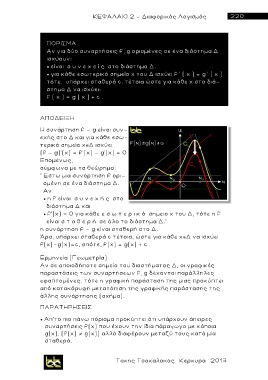
Ερμηνεία (Γεωμετρία)

Αν σε οποιοδήποτε σημείο του διαστήματος Δ, οι γραφικές

παρασ τ άσεις των συναρτήσεων f, g δέχονται παράλληλες
εφαπτομένες, τότε η γραφική παράσταση της μιας προκύπτει

α π ό κατακόρυφη μετατόπιση της γραφικής παράστασης της

άλλης συνάρτησης (σχήμα).

ΠΑΡΑΤΗΡΗΣΕΙΣ

 Aπ’το πιο πάνω πόρισμα προκύπτει ότι υπάρχουν άπειρες

συναρτήσεις f(x) που έχουν την ίδια πάραγωγο με κάποια
g(x), (f(x) g(x)) αλ λ ά διαφέρουν μεταξύ τους κατά μία

σταθερά.

Τακης Τσακαλακος Κερκυρα 2017