Page 221 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 221

 Το παραπάνω πόρισμα ισχύει σε διάστημα και όχι σε ένωση
δ ι αστημάτων
(ισχύει όμως σε κάθε διάστημα χωριστά)

 Ισχύει και το αντίστροφο του παραπάνω πορίσματος.

ΒΑΣΙΚΗ ΠΡΟΤΑΣΗ
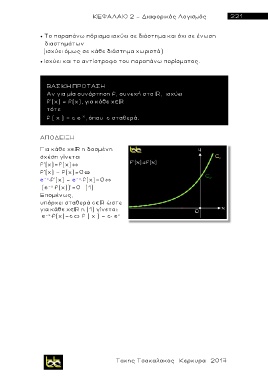
Αν για μία συνάρτηση f, συνεχή στο , ισχύει
f’ ( x) = f(x), για κ ά θ ε x

τότε
f ( x ) = c e , όπου c σταθερά.
x

ΑΠΟΔΕΙΞΗ

Για κάθε χ η δοσμένη

σχέση γίνεται

f’ ( x)=f(x)`
f’ ( x) - f(x)=0`

e - x f’ ( x) - e - x f(x)=0`

(e - x f(x))’=0 (1)
Επομένως,

υπάρχει σταθερά c ώστε

για κάθε x η (1) γίνεται:
x
e - x f(x)=c` f ( x ) = c e

Τακης Τσακαλακος Κερκυρα 2017