Page 224 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 224

2. ΑΠΟΔΕΙΞΗ: ΣΤΑΘΕΡΗ ΣΥΝΑΡΤΗΣΗ
(ΕΝΩΣΗ ΔΙΑΣΤΗΜΑΤΩΝ)
Δίνεται η παραγωγίσιμη συνάρτηση f: * , για την οποία
ισχύει
f(x)
f'(x)=-2 x για κάθε χ *
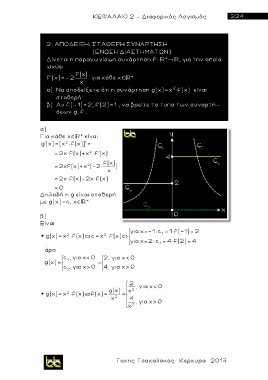
α) Nα αποδείξετε ότι η συνάρτηση g(x)=x 2 f(x) είναι

σταθερή
β) Αν f(-1)=2, f(2)=1 , να βρείτε το τυπο των συναρτή-
σεων g, f .

α )
Για κάθε χ * είναι
g'(x) =[x × f(x) ]' =
2
2
= 2x× f(x) +x × f'(x)
f(x)
= 2xf(x) +x (-2× )
2
x
= 2x× f(x) -2x× f(x)

= 0
Δηλαδή η g είναι σταθερή
με g(x)=c, χ *

β )
Είναι

g(x)= χ 2 f(x) ` c= χ 2 f(x) ` για χ = -1: c = 1 f(-1)= 2
1
για χ = 2: c = 4 f(2)= 4
1
άρα
c , για χ < 0 2 , για χ < 0
g(x) = 1
c , για χ > 0 4, για χ > 0
2

2 , για χ < 0
g(x)= χ 2 f(x) ` f(x)= g(x) χ 2
χ 2 4 , για χ > 0
χ 2

Τακης Τσακαλακος Κερκυρα 2017