Page 23 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 23

2.
Να μελετήσετε ως προς τη συνέχεια στη θέση x 0 και στη
συνέχεια να εξετάσετε αν είναι παραγωγίσιμες στη θέση
αυτή οι συναρτήσεις
α) f(x)=| χ-κ | -κ, x 0 = κ
x -x+2 x 0
2
β ) g(x)= , x = 0
x+ln(x+1)+3 x> 0 0

α )
Είναι Α f =

f(κ)=| -κ| +κ= κ (1)

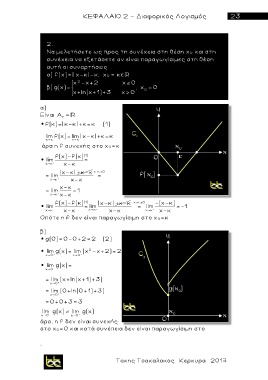
lim f(x)= lim | x-κ| +κ= κ
x → x →
άρα η f συνεχής στο χ 0= κ

x f(x)-f(κ) (1)
=
lim

x-κ
→

=
= lim | x-κ| +κ-κ x -κ 0
→
x x-κ
x-κ
lim 1
→
x κ x-κ
f(x)-f(κ) (1) | x-κ| +κ-κ x -κ 0 -(x-κ)
x x-κ = lim x-κ = x κ x-κ 1
lim
lim

→
x
→
→
Οπότε η f δεν είναι παραγωγίσιμη στο χ 0=κ

β )
g(0)= 0 0+2= 2 (2)

lim g(x)= lim ( χ -x+2)= 2
2
x 0 x 0
→
→
lim g(x)=
x 0
→

= lim ( χ+ln(x+1)+3)
x 0
→

= lim ( 0+ln(0+1)+3)
x 0
→

= 0+0+3= 3
lim g(x) ô lim g(x)

x 0 x 0
→
→
άρα, η f δεν είναι συνεχής

στο χ 0=0 και κατά συνέπεια δεν είναι παραγωγ ί σιμη στο

.
Τακης Τσακαλακος Κερκυρα 2017