Page 254 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 254

Θ Ε Ω Ρ Ι Α ...

ΘΕΩΡΗΜΑ
Έστω η συνάρτηση f που είναι σ υ ν ε χ ή ς σ’ενα διάστημα
Δ
 f ’ ( x ) > 0 σε κάθε ε σ ω τ ε ρ ι κ ό σημείο του Δ, τότε η
f είναι γ ν ή σ ι α α ύ ξ ο υ σ α σ'όλο το διάστημα Δ.
 f ’ ( x ) < 0 σε κάθε ε σ ω τ ε ρ ι κ ό σημείο του Δ, τ' ο τε η
f είναι γ ν ή σ ι α φ θ ί ν ο υ σ α σ'όλο το διάστημα Δ.

ΑΠΟΔΕΙΞΗ

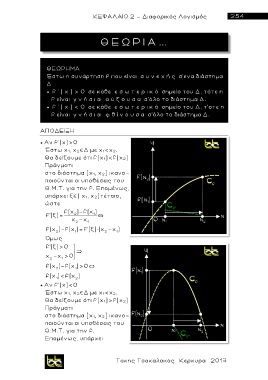
 Aν f'(x)>0

Έστω χ 1, χ 2 Δ με χ 1< χ 2.
Θα δείξουμε ότι f(x 1)<f(x 2)

Πράγματι
στο διάστημα [χ 1, χ 2] ικανο-
ποιούνται οι υπ ο θέσεις του

Θ.Μ.Τ. για την f. Επομένως,

υπάρχει ξ ( χ 1, χ 2)τέτοιο,
ώστε

f(x )-f(x )
f'(ξ) 2 1 `
x -x 1
2
f(x )-f(x )= f'(ξ) (x -x )
1
1
2
2

Όμως
f'(ξ)> 0 ~
x -x 0
2 1
f(x )-f(x ) 0 `
2 1
f(x )< f(x )
1 2
 Aν f'(x)<0
Δ με χ 1< χ 2.
Έστω χ 1, χ 2
Θα δείξουμε ότι f(x 1)>f(x 2)

Πράγματι

στο διάστημα [χ 1, χ 2] ικανο-
ποιούνται οι υπ ο θέσεις του

Θ.Μ.Τ. για την f.

Επομένως, υπάρχει

Τακης Τσακαλακος Κερκυρα 2017