Page 255 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 255

ξ ( χ 1, χ 2)τέτοιο, ώστε
f(x )-f(x )
f'(ξ) 2 1 ` f(x )-f(x )=f'(ξ) (x -x )
x -x 1 2 1 2 1
2
Όμως
f'(ξ)< 0
~ f(x )-f(x ) 0 ` f(x )> f(x )
x -x 0 2 1 1 2
2 1

ΠΑΡΑΤΗΡΗΣΕΙΣ

● Το αντίστροφο του θεωρή-
ματος δεν ισχύει.

Μπορεί η f να είναι γνησί-
ω ς μονότονη σε διάστημα
Δ, αλ λ ά η f' να μη διατηρεί
π ρ όσημο στο Δ και να έχει
σημεία μηδενισμού.
Παραδειγμα
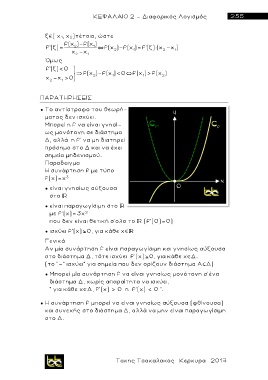
Η συνάρτηση f με τύπο
f(x)=x
3
● είναι γνησίως αύξουσα
στο

● είναι παραγωγίσιμη στο
με f'(x)=3x
2
που δεν είναι θετική σ'ολο το (f'(0)=0)

● ισχύει f'(x) 0, για κάθε χ

Γενικά
Αν μία συνάρτηση f είναι παραγωγίσιμη και γνησίως αύξουσα
στο διάστημα Δ, τότε ισχύει f'(x) 0, για κάθε χ Δ.
(το "=" ισχύει" για σημεία που δεν ορίζουν διάστημα Α Δ )

● Μπορεί μία συνάρτηση f να είναι γνησίως μονότονη σ’ένα
διάστημα Δ, χωρίς απαραίτητα να ισχύει,
“ για κάθε x Δ, f’ ( x) > 0 η f’ ( x) < 0 ”.

● H συνάρτηση f μπορεί να είναι γνησίως αύξουσα (φθίνουσα)
και συνεχής στο διάστημα Δ, αλλά να μην είναι παραγωγίσιμη
στο Δ.

Τακης Τσακαλακος Κερκυρα 2017