Page 259 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 259

[β, γ]=[α, β]∪[β, γ]
 Όμοια, αν η f είναι γνησίως φθίνουσα σ τ α διαστήματα [α, β]
και [β, γ].
 Για ανοικτά διασ τ ήματα ισχύει μόνο αν η f είναι συνεχής στο
β .

4.
Αν μία συνάρτηση f είναι γνησίως αύξουσα (φθίνουσα) στο

διάστημα [α, β], τότε η εξίσωση f(x)=κ έχει μία το πολύ
λύση στο διάστημα [α, β].

ΑΠΟΔΕΙΞΗ

 H f είναι γνησίως αύξουσα

(φθίνουσα) στο διάστημα

[α, β], συνεπώς η f είναι
"1-1", στο διάστημα αυτό.

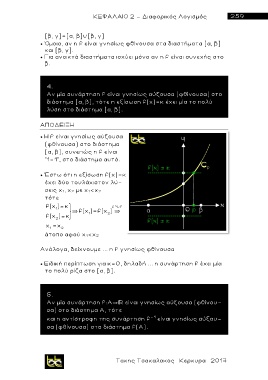
 Έστω ότι η εξίσωση f(x)=κ

έχει δύο τουλάχιστον λύ-
σεις χ 1, χ 2 με χ 1< χ 2

τότε
f(x ) f "1 -1"
1

1
2
f(x ) ~f(x ) f(x ) ~
2
x 1 x 2
άτοπο αφού χ 1<χ 2

Ανάλογα, δείχνουμε ... η f γνησίως φθίνουσα

 Ειδική περίπτωση για κ=0, δηλαδή ... η συνάρτηση f έχει μία

το πολύ ρίζα στο [α, β].

5.
Αν μία συνάρτηση f:Α είναι γνησίως αύξουσα (φθίνου-

σα) στο διάστημα Α, τότε
και η αντίστροφη της συνάρτηση f - 1 είναι γνησίως αύξου-
σα (φθίνουσα) στο διάστημα f(A).

Τακης Τσακαλακος Κερκυρα 2017