Page 266 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 266

3. ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ (ΠΑΡΑΜΕΤΡΟΣ)
Να προσδιοριστεί η παράμετρος α, ώστε η συνάρτηση f, με
τύπο f(x)=-x +(2α-1)x -3x+2
2
3

να είναι γνησίως φθίνουσα στο .

● H f είναι γνησίως φθίνου-
σα στο
οπότε πρέπει να ισχύει
f'(x)<0 για κάθε χ
Έτσι

f'(x)<0
(-x +(2α-1)x -3x+2)'<0
2
3
-x +2 (2α-1)x-3<0 (1)
2
● Για να είναι αρνητικό το
τριωνυμο
-x +2 (2α-1)x-3,
2
για κάθε χ
πρέπει
Δ 0~[2(2α-1)] -4(-3)(-3) 0
2
2
~16α -16α+4-36 0
~ α -α-2 0
2
~(α+1)(α-2) 0

~ -1 α 2

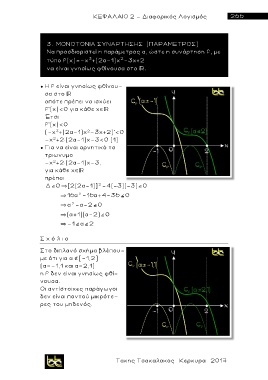
Σ χ ό λ ι ο

Στο διπλανό σχήμα βλέπου-
με ότι για α [-1,2]

(α=-1,1 και α=2,1)
η f δεν είναι γνησίως φθί-
νουσα.
Οι αντίστοιχες παράγωγοι
δεν είναι παντού μικρότ ε -
ρες του μηδενός.

Τακης Τσακαλακος Κερκυρα 2017