Page 271 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 271

2. ΠΛΗΘΟΣ ΡΙΖΩΝ (f(χ)=κ)
Δίνεται η συνάρτηση f με τύπο f(x)=x lnχ, χ (0, + )
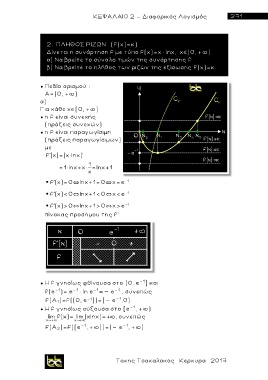
α) Να βρείτε το σύνολο τιμών της συνάρτησης f
β) Να βρείτε το πλήθος των ριζών της εξίσωσης f(χ)=κ.

● Πεδίο ορισμού :
Α=(0, + )
α )
Για κάθε χ [0, + )
● η f είναι συνεχής

(πράξεις συνεχών)
● η f είναι παραγωγίσιμη
(πράξεις παραγωγίσιμων)
μ ε
f'(x)=(x lnx)'
1
= 1 lnx+x = lnx+1
x

f'(x)= 0 ` lnx+1= 0 ` x= e 1

f'(x)< 0 ` lnx+1< 0 ` x< e 1

f'(x)> 0 ` lnx+1> 0 ` x> e 1

πίνακας προσήμου της f'

● H f γνησίως φθίνουσα στο (0, e - 1 ] και

f(e - 1 )= e - 1 ln e -1 =- e - 1 , συνεπώς
f(Α 1 )=f((0, e - 1 ])=[- e - 1 ,0)
● H f γνησίως αύξουσα στο [e - 1 , + )

lim f(x)= lim (xlnx)=+ , συνεπώς
x + x +
f(Α 2 )=f([e -1 , + ))=(- e -1 , + )

Τακης Τσακαλακος Κερκυρα 2017