Page 273 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 273

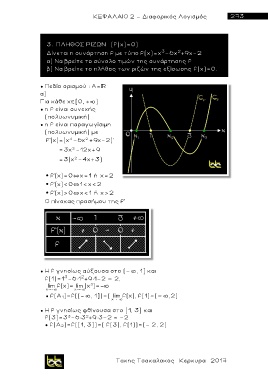
3. ΠΛΗΘΟΣ ΡΙΖΩΝ (f(χ)=0)
Δίνεται η συνάρτηση f με τύπο f(x)=x -6χ +9χ-2
3
2

α) Να βρείτε το σύνολο τιμών της συνάρτησης f
β) Να βρείτε το πλήθος των ριζών της εξίσωσης f(χ)=0.

● Πεδίο ορισμού : Α=
α )
Για κάθε χ [0, + )
● η f είναι συνεχής
(πολυωνυμική)

● η f είναι παραγωγίσιμη
(πολυωνυμική) με
3
f'(x)=(x -6χ +9χ-2)'
2
= 3χ -12x+9
2
= 3(χ -4x+3)
2

f'(x)= 0 ` x= 1 ή χ= 2
f'(x)< 0 ` 1< x< 2

f'(x)> 0 ` x< 1 ή χ> 2

Ο πίνακας προσήμου της f'

● H f γ ν η σ ίως αύξουσα στο (- , 1] και
3
2
f(1)=1 -6 1 +9 1-2 = 2,
lim f(x)= lim (x )=-
3
x - x -
● f(Α 1 )=f((- , 1])=( lim f(x), f(1)=(- ,2)
x -

● H f γνησίως φθίνουσα στο [1, 3] και
f(3)=3 -6 3 +9 3-2 = -2
2
3
● f( Α 2)=f([1, 3])=( f(3), f(1))=(- 2, 2)

Τακης Τσακαλακος Κερκυρα 2017