Page 276 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 276

ΠΑΡΑΔΕΙΓΜΑΤΑ

1. ΑΠΟΔΕΙΞΗ ΑΝΙΣΩΣΗΣ
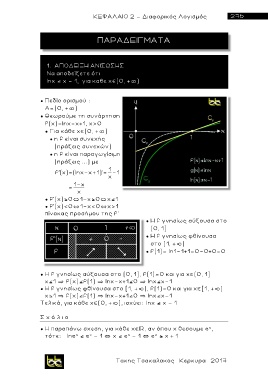
Να αποδείξετε ότι
lnχ x - 1, για καθε χ (0, + )

● Πεδίο ορισμού :
Α=(0, + )
● Θεωρούμε τη συνάρτηση
f(x)=lnx-x+1, x>0
● Για κάθε χ (0, + )

● η f είναι συνεχής
(πράξεις συνεχών)
● η f είναι παραγωγίσιμη
(πράξεις ...) με
1
f'(x)=(lnx-x+1)' = -1
x
= 1-x
x
● f'(x) 0`1-x 0`x 1
● f'(x)<0`1-x<0`x>1
πίνακας προσήμου της f'
● H f γνησίως αύξουσα στο

(0, 1]
● H f γνησίως φθίνουσα
στο [1, + )

● f(1)= ln1-1+1=0-0+0=0

● H f γνησίως αύξουσα στο (0, 1], f(1)=0 και για χ (0, 1]
χ 1 ~ f(x) f(1) ~ lnx-x+1 0 ~ lnx x-1
● H f γνησίως φθίνουσα στο [1, + ), f(1)=0 και για χ [1, + )
χ 1 ~ f(x) f(1) ~ lnx-x+1 0 ~ lnx x-1
Τελικά, για κάθε χ (0, + ), ισχύει: lnχ x - 1

Σ χ ό λ ι ο

● H παραπάνω σχεση, για κάθε χ , αν όπου χ θεσουμε e ,
x
τότε: lne e - 1 ` x e - 1 ` e x + 1
x
x
x
x

Τακης Τσακαλακος Κερκυρα 2017