Page 281 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 281

ΠΑΡΑΔΕΙΓΜΑΤΑ

1. ΑΠΟΔΕΙΞΗ ΑΝΙΣΩΣΗΣ (ΠΑΡΑΜΕΤΡΙΚΗ)
Να αποδείξετε ότι
α-1
αν α<β<1, τοτε e α -β < β-1

● Είναι :
α-1
e α -β < ~
β-1
α-1
+
e α -1 1 -β < ~
β-1

e (α -1) - (β -1) < α-1 ~
β-1

e α -1 < α-1 ~ e α -1 < e β -1
e β -1 β-1 α-1 β-1

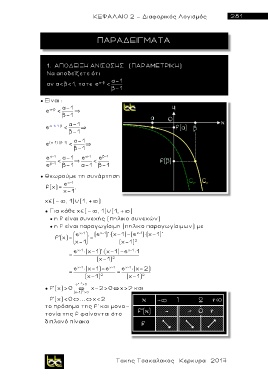
● Θεωρούμε τη συνάρτηση
e χ -1
f(x)= ,
χ-1

x (- , 1)∪(1, + )
● Για κάθε x (- , 1)∪(1, + )

● η f είναι συνεχής ( π ηλικο συνεχών)
● η f είναι παραγωγίσιμη (πηλικο παραγωγίσιμων) με
e χ -1 (e χ -1 )' (χ-1)-(e χ -1 ) (χ-1)'
f'(x)= '
χ-1 (χ-1) 2

e χ -1 (χ-1)' (χ-1)-e χ -1 1

(χ-1) 2
e χ -1 (χ-1)-e χ -1 e χ -1 (χ-2)

(χ-1) 2 (χ-1) 2
e x-1 > 0
● f'(x)>0 ` χ-2>0`x>2 και
2
(x -1) > 0
f'(x)<0`...`x<2
τ ο π ρ όσημο της f' και μονο-
τονία της f φαίνονται στο
διπλανό πίνακα

Τακης Τσακαλακος Κερκυρα 2017