Page 284 - diaforikos
P. 284
ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 284
3. ΑΠΟΔΕΙΞΗ ΑΝΙΣΩΣΗΣ (ΠΑΡΑΜΕΤΡΙΚΗ)
Να αποδείξετε ότι
α+β α β
αν 0<α<β, τοτε ln 2 < α+β ln α+β ln
Είναι :
α+β α β α > 0
ln < ln ln ~
2 α+β α+β β > 0
α+β
(α+β ) ln < α ln β ln ~
2
α+β
(α+β )ln -α ln β ln < 0
2
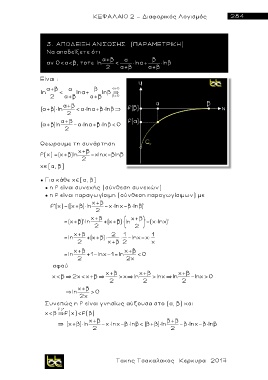
Θεωρουμε τη συνάρτηση
χ+β
f(x) (χ+β )ln -χln βln ,
2
χ [α, β]
● Για κάθε χ [α, β]
● η f είναι συνεχής (σύνθεση συνεχών)
● η f είναι παραγωγίσιμη (σύνθεση παραγωγίσιμων) με
χ+β
f'(x)=( (χ+β ) ln -χ ln β ln )'
2
χ+β χ+β
=(χ+β )' ln (χ+β ) ln '-(χ ln )'
2 2
= ln χ+β (χ+β ) 2 1 -ln 1
2 χ+β 2
χ+β χ+β
= ln 1-ln 1= ln 0
2 2χ
αφού
χ+β χ+β χ+β
χ< β~2χ< χ+β~ χ ~ln lnχ~ln lnχ 0
2 2 2
~ln χ+β 0
2χ
Συνεπώς η f είναι γνησίως αύξουσα στο (α, β) και
f
χ<β ~f(x)<f(β)
χ+β β+β
~ (χ+β) ln -χ ln β ln < (β+β) ln -β ln β ln
2 2
Τακης Τσακαλακος Κερκυρα 2017