Page 287 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 287

ΠΑΡΑΔΕΙΓΜΑΤΑ

1. ΠΡΟΒΛΗΜΑ (ΦΥΣΙΚΗ)
Όχημα κινείται πάνω σε άξονα και η θέση του κάθε χρονική
στιγμή δίνεται απ'τη συνάρτηση:
t 3
2
χ(t)= 3 -2t +3t+1 (1), t 0 με t σε sec.
a) Πότε το όχημα απομακρύνεται από την εφετηρία και πό -
τε επιστρέφει σε αυτήν;
β) Πότε ο οδηγός "φρενάρει" και πότε "γκαζών ει" το όχημα;

γ) Πότε το όχημα σταματάει στιγμιαία;
δ) Ποιά χρονική στιγμή το όχημα επιστρέφει στην αφετηρία;

● Ανεξάρτητη μεταβλητή:
ο χρόνος t
● υ ( t)=x'(t) η ταχύτητα ή
ο ρυθμός μεταβολής της
θέσης
● α ( t) =υ'(t)=x''(t) η επι-
τάχυνση ή ο ρυθμός με-
ταβο λ ής της ταχύτητας
υ(t)= x'(t)

● t 3
= -2t +3t+1 '
2
3
2
t -4t+3
● υ(t) 0~ t -4t+3 0~1 t 3(*)
2
2
● α(t)=υ'(t)= t -4t+3 ' =2t-4
α)
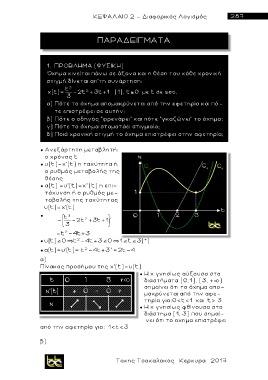
Πίνακας προσήμου της χ'(t)=υ(t)
● H χ γνησίως αύξουσα στα
διασ τ ήμ α τα [0,1], [3, + )
σημαίνει ότι το όχημα απο-
μακρύνεται από την αφε-
τηρία για:0<t<1 και t> 3
● H χ γνησίως φθίνουσα στο
διάστημα [1, 3] που σημαί-

νει ότι το οχημα επιστρέφει
α π ό την αφετηρία για: 1<t<3

β)

Τακης Τσακαλακος Κερκυρα 2017