Page 289 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 289

2. ΠΡΟΒΛΗΜΑ (ΟΙΚΟΝΟΜΙΑ)
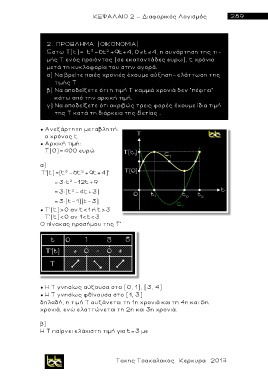
Έστω Τ(t)= t -6t +9t+4, 0 t 4, η συνάρτηση της τι-
3
2
μής Τ ενός προιόντος (σε εκατοντάδες ευρω), t χρόνια
μετά τη κυκλοφορία του στην αγορά.
a) Να βρείτε ποιές χρονιές έχουμε αύξηση-ελάττωση της
τιμής Τ

β) Να αποδείξετε ότι η τιμή Τ καμμιά χρονιά δεν "πέφτει"
κάτω από την αρχική τιμή.
γ) Να αποδείξετε ότι ακριβώς τρεις φορές έχουμε ίδια τιμή
της Τ κατά τη διάρκεια της 5ετίας .

● Ανεξάρτητη μεταβλητή:
ο χρόνος t
● Αρχική τιμή:
Τ(0)=400 ευρώ

α )
3
2
T'(t)= (t -6t +9t+4)'
2
= 3× t -12t+9

= 3×(t -4t+3)
2
= 3×(t-1)(t-3)
● Τ'(t)>0 aν t<1 ή t>3
Τ'(t)<0 aν 1<t<3
Ο πίνακας προσήμου της Τ'

● H Τ γνησίως αύξουσα στα [0, 1], [3, 4]
● H Τ γνησίως φθίνουσα στο [1, 3]
δηλαδή, η τιμή Τ αυξάνεται τη 1η χρονιά και τη 4η και 5η
χρονιά, ενώ ελαττώνεται τη 2η και 3η χρονιά.

β)
Η Τ παίρνει ελάχιστη τιμή για t=3 με

Τακης Τσακαλακος Κερκυρα 2017