Page 292 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 292

ΠΑΡΑΔΕΙΓΜΑΤΑ

1. ΕΠΙΛΥΣΗ ΕΞΙΣΩΣΗΣ
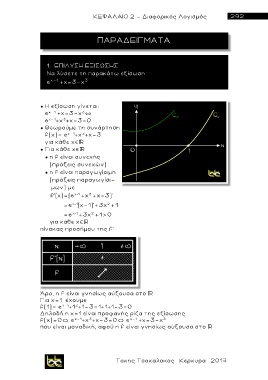
Να λύσετε τη παρακάτω εξίσωση
e x- 1 +x=3-x
3

● Η εξίσωση γίνεται:
e x - 1 +x=3-x `
3
e x - 1 +x +x-3=0
3
● Θεωρούμε τη συνάρτηση
f(x)= e x - 1 +x +x-3
3
για κάθε χ
● Για κάθε χ
● η f είναι συνεχής

(πράξεις συνεχών)
● η f είναι παραγωγίσιμη
(πράξεις παραγωγίσι-
μων) με
f'(x)=(e x -1 +x +x-3 )'
3
= e x -1 (x-1 )' +3x +1
2
= e x -1 +3x +1> 0
2
για κάθε χ
πίνακας προσήμου της f'

Άρα, η f είναι γνησίως αύξουσα στο
Για χ=1 έχουμε
f(1)= e 1 - 1 +1 +1-3=1+1+1-3=0
3
Δηλαδή η χ=1 είναι προφανής ρίζα της εξίσωσης
f(x)=0` e x - 1 +x +x-3=0` e x - 1 +x=3-x
3
3
που είναι μοναδική, αφού η f είναι γνησίως αύξουσα στο

Τακης Τσακαλακος Κερκυρα 2017