Page 295 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 295

4. ΕΠΙΛΥΣΗ ΕΞΙΣΩΣΗΣ
Αν η συνάρτηση f είναι παραγωγίισιμη στο διάστημα [1, e]
με 0 < f(x) < 1 και f'(x) ≥ 0 για καθε x [1, e], να δειχθεί
ότι υπάρχει μόνο ένα x 0 (1, e) τέτοιο, ώστε:

f(x 0 ) + x 0 ∙ lnx 0 = x 0

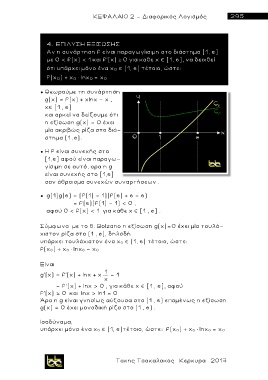
● Θεωρούμε τη συνάρτηση
g(x) = f(x) + xlnx - x ,

x [1 , e]
και αρκεί να δείξουμε ότι
η εξίσωση g(x) = 0 έχει
μία ακριβώς ρίζα στο διά-
στημα (1 ,e).

● Η f είναι συνεχής στο
[1,e] αφού είναι παραγω-
γίσιμη σε αυτό, αρα η g
είναι συνεχής στο [1,e]
σαν άθροισμα συνεχών συναρτήσεων .

● g(1)g(e) = (f(1) - 1)(f(e) + e - e)
= f(e)(f(1) - 1) < 0 ,
αφού 0 < f(x) < 1 για κάθε x [1 , e] .

Σύμφωνα με το θ. Bolzano η εξίσωση g(x)=0 έχει μία τουλά-
χιστον ρίζα στο (1 , e), δηλσδή
υπάρχει τουλάχιστον ένα x 0 (1, e) τέτοιο, ώστε:
f(x 0) + x 0 ∙ lnx 0 = x 0

Είναι
1
g’(x) = f’(x) + lnx + x - 1
x
= f΄(x) + lnx > 0 , για κάθε x [1 , e], αφού
f'(x) 0 και lnx > ln1 = 0
Άρα η g είναι γνησίως αύξουσα στο (1 , e) επομένως η εξίσωση
g(x) = 0 έχει μοναδική ρίζα στο (1 , e) .

Ισοδύναμα,
υπάρχει μόνο ένα x 0 (1, e)τέτοιο, ώστε: f(x 0) + x 0 ∙ lnx 0 = x 0

Τακης Τσακαλακος Κερκυρα 2017