Page 299 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 299

2. ΕΠΙΛΥΣΗ ANΙΣΩΣΗΣ
Δίνεται η συνάρτηση f με τύπο f(x)=3+ x 1 , x 3
α) Να αποδείξετε ότι η f αντιστρέφεται
-1
β) Να λύσετε την ανίσωση f (x)<2x-5

α )
● Για κάθε χ [1, + )
● η f είναι συνεχής
(πράξεις συνεχών)
● η f είναι παραγωγίσιμη
(πράξεις παραγωγίσι-

μων) με
(x-1 )'
f'(x)=( 3+ x-1 )' =
2 x-1
= 1 0
2 x-1
για κάθε χ [1, + )
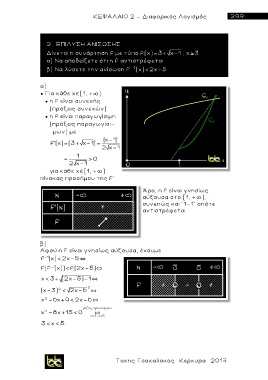
πίνακας προσήμου της f'

Άρα, η f είναι γνησίως
αύξουσα στο [1, + ),
συνεπώς και "1-1" οπότε
αντιστρέφεται

β )
Αφού η f είναι γνησίως αύξουσα, έχουμε

-1
f (x)< 2x-5`
f(f (x))< f(2x-5) `
-1
x< 3+ (2x-5)-1 `

2
(x-3) < 2x-6 `
2
x -6x 9 < 2x-6 `
2
ρίζες τριωνύμου
x -8x 15< 0 `
2
χ =3, χ =5
3< x< 5

Τακης Τσακαλακος Κερκυρα 2017