Page 294 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 294

3. ΕΠΙΛΥΣΗ ΕΞΙΣΩΣΗΣ
Να λύσετε τη παρακάτω εξίσωση
ln(x +1)=ln(χ +χ+1)+x
2
2

● Προσθέτουμε στην εξί-
σωση τη ποσότητα χ +1
2
και προκύπτει:
ln(x +1)+ χ +1 =
2
2
=ln(χ +χ+1)+x+ χ +1 `
2
2
ln(x +1)+ (χ +1) =
2
2
=ln(χ +χ+1)+(x + χ+1) (1)
2
2

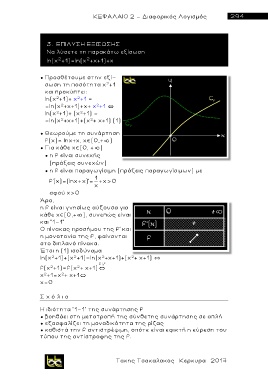
● Θεωρούμε τη συνάρτηση
f(x)= lnx+x, χ (0,+ )
● Για κάθε χ (0, + )
● η f είναι συνεχής
(πράξεις συνεχών)
● η f είναι παραγωγίσιμη (πράξεις παραγωγίσιμων) με
1
f'(x)=( lnx+x)' = +x 0
x
αφού χ>0
Άρα,
η f είναι γνησίως αύξουσα για
κάθε χ (0,+ ), συνεπώς είναι
και "1-1"
O πίνακας προσήμου της f' και
η μονοτονία της f, φαίνονται
στο διπλανό πίνακα.
Έτσι η (1) ισοδύναμα
ln(x +1)+(χ +1)=ln(χ +χ+1)+(x + χ+1) `
2
2
2
2
f
2
2
f(x +1)=f(x + χ+1) `
2
2
x +1=x + χ+1`
x=0

Σ χ ό λ ι ο
Η ιδιότητα "1-1" της συνάρτησης f
● βοηθάει στη μετατροπή της σύνθετης συνάρτησης σε απλή
● εξασφαλίζει τη μοναδικότητα της ρίζας
● καθιστά την f αντιστρέψιμη, οπότε είναι εφικτή η εύρεση του
τύπου της αντίστροφης της f.

Τακης Τσακαλακος Κερκυρα 2017