Page 283 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 283

2. ΑΠΟΔΕΙΞΗ ΑΝΙΣΩΣΗΣ (ΒΟΗΘΗΤΙΚΗ ΣΥΝΑΡΤΗΣΗ)
π εφα α
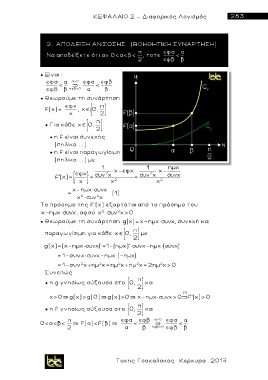
Να αποδείξετε ότι αν 0<α<β< 2 , τοτε εφβ < β

● Είναι :
εφα α α > 0 εφα εφβ
< ~ <
εφβ β εφβ > 0 α β
● Θεωρούμε τη συνάρτηση
εφχ π
f(x)= , χ 0,
χ 2

π
● Για κάθε χ 0,
2
● η f είναι συνεχής
(πηλίκο ...)
● η f είναι παραγωγίσιμη
(πηλίκο ...) με
1 1 ημχ
εφ x 2 x-εφχ 2 x-
f'(x)= ' = =
x x 2 x 2

x-ημχ
= (1)
x 2 2
Το πρόσημο της f'(x) εξαρτάται από το πρόσημο του
x-ημχ , αφού x 2 2 0
● Θεωρούμε τη συνάρτηση g(x)=x-ημχ , συνεχή και

π
παραγωγίσιμη για κάθε χ 0, με
2
g'(x)=(x-ημχ )' 1-(ημχ)' -ημχ ( )'

= 1-συνχ -ημχ (-η μ )
= 1-συν χ+ημ χ= ημ χ+ημ χ= 2ημ χ> 0
2
2
2
2
2
Συνεπώς
π
● η g γνησίως αύξουσα στο 0, και
2
(1)
χ > 0~g(x)>g(0)~g(x)>0~ x-ημχ >0~f'(x)>0
π
● η f γνησίως αύξουσα στο 0, και
2
π εφα εφβ α > 0 εφα α
0<α<β< ~ f(a)<f(β)~ < ~ <
2 α β εφβ > 0 εφβ β

Τακης Τσακαλακος Κερκυρα 2017