Page 279 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 279

4. ΑΠΟΔΕΙΞΗ ΑΝΙΣΩΣΗΣ
Να αποδείξετε ότι
e ex, για καθε χ (0, + )
χ

● Πεδίο ορισμού :
Α=(0, + )
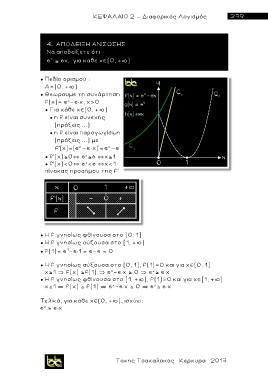
● Θεωρουμε τη συνάρτηση
f(x)= e -e x, x>0
χ
● Για κάθε χ (0, + )

● η f είναι συνεχής
(πράξεις ...)
● η f είναι παραγωγίσιμη
(πράξεις ...) με
χ
)'
f'(x)=( e -e x =e -e
χ
● f'(x) 0` e χ e `x 1
● f'(x)<0` e <e `x<1
χ
πίνακας προσήμου της f'

● H f γνησίως φθίνουσα στο (0, 1]
● H f γνησίως αύξουσα στο [1, + )
1
● f(1)= e -e 1 = e-e = 0

● H f γνησίως αύξουσα στο (0, 1], f(1)=0 και για χ (0, 1]
χ 1 ~ f(x) f(1) ~ e -e x 0 ~ e χ e x
χ
● H f γνησίως φθίνουσα στο [1, + ), f(1)=0 και για χ [1, + )
χ 1 ~ f(x) f(1) ~ e -e x 0 ~ e χ e x
χ

Τελικά, για κάθε χ (0, + ), ισχύει:
e χ e x

Τακης Τσακαλακος Κερκυρα 2017