Page 32 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 32

3.
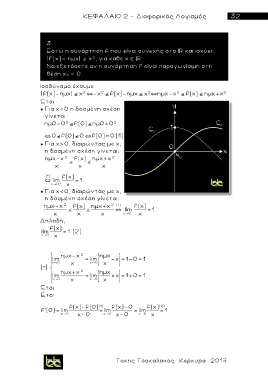
Εστω η συνάρτηση f που είναι συνεχής στο και ισχύει:
|f(x)- ημχ| º χ , για καθε x
2
Να εξετάσετε αν η συνάρτηση f είναι παραγωγίσιμη στη
θέση x 0 = 0.

Ισοδύναμα έχουμε

|f(x)-ημχ| χ ` -χ 2 f(x)-ημχ χ ` ημχ-χ 2 f(x) ημχ χ
2
2
2
Έτσι

● Για χ=0 η δοσμένη σχέση

γίνεται
ημ0-0 2 f(0) ημ0+0 2

0 f(0) 0 f(0)=0 (1)
● Για χ>0, διαιρώντας με χ,

η δοσμένη σχέση γίνεται:

ημx-x 2 f(x) ημx+x 2
x x x

( * ) lim f(x) = 1
x 0 + x
● Για χ<0, διαιρώντας με χ,

η δοσμένη σχέση γίνεται:

ημx-x 2 f(x) ημx+x 2 ( * ) lim f(x) =1

x x x x 0 - x

Δηλαδή,

lim f(x) = 1 (2)
x 0 x

ημx-x 2 ημx
lim = lim -x = 1-0= 1

(*) x 0 x 2 x 0 x
lim
x 0 ημx+x = lim ημx +x = 1+0= 1
x
x
x 0

Έτσι
Ετσι

f(x)-f(0) ( 1 ) f(x)-0 f(x) ( 2 )
f '(0) = lim x-0 = lim x-0 = lim x = 1

x 0
x 0
x 0

Τακης Τσακαλακος Κερκυρα 2017