Page 36 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 36

2.
Για τη πραγματική συνάρτηση f, που είναι συνεχής στη
f(3-χ)
θέση x 0 = 3, ισχύει: lim x =1
x 0
Να απόδειξετε ότι η συνάρτηση f είναι παραγωγίσιμη στη
θέση x 0 = 3.

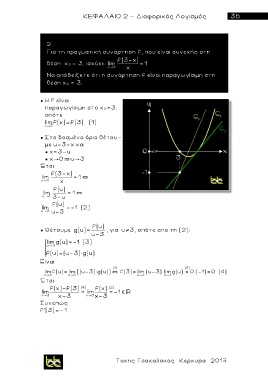
● Η f είναι

παραγωγίσιμη στο χ 0=3,

οπότε
lim f(x)=f(3) (1)

x 3

● Στο δοσμένο όριο θέτου-
με u=3-x και

● χ=3-u

● χ 0~u 3
Έτσι

lim f(3-χ) = 1 `
x 0 x

lim f(u) = 1 `
u 3 3-u
f(u)
lim =-1 (2)
u 3 u-3

● Θέτουμε g(u)= f(u) , για u 3, οπότε απο τη (2):
lim g(u)=-1 (3) u-3

u 3
f(u)=(u-3)× g(u)

Είναι
(1) (3)
lim f(u)= lim [(u-3)× g(u)] ` f(3)= lim (u-3)× lim g(u) = 0×(-1)= 0 (4)
u
3
u
3
u
3
u
3
Έτσι

(4)
(2)
lim f(x)-f(3) = lim f(x) = 1

x 3 x-3 x 3 x-3
Συνεπώς

f'(3)=-1

Τακης Τσακαλακος Κερκυρα 2017