Page 41 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 41

Οπότε ο τύπος της h είναι
-2χ+3, αν χ< 1

h(x)= 1 , αν 1ºχ< 2
2χ-3 , αν χ 2
Στο χ 1 1

lim h(x)= lim(-2x+3)= 1
h(1)= 1 (3) x 1→ x 1→ η h συνεχής στα χ=1
lim h(x)= lim(2x-3)= 1
x 2→ x 2→
h(x)-h(x ) (3) 1-1
lim 0 = lim = 0
x 1→ x-x x 1→ x-1
0
και χ=2
(3)
lim h(x)-h(x ) =
0
→
x 1 x-x 0
-2χ+3-1
lim =
x 1 x-1
→
-2χ+2
lim =
x 1 x-1
→

-2(χ-1)
lim =
x 1 x-1
→
lim ( -2)=-2
→
x 1

h(x)-h(1) h(x)-h(1)
lim lim
ô
x 1 x-1 x 1 x-1
→
→
Συνεπώς η h δεν είναι παραγωγίσιμη στο χ 1=1
Στο χ 2 2

h(2)= 4-3= 1 (4)
h(x)-h(x ) (4) 2χ-3-1 2χ-4 2(χ-2)
lim 0 = lim = lim = lim = 2
→
x 2 x-x x 2 x-2 x 2 x-2 x 2 x-2
→
→
→
0
h(x)-h(x ) (4) 1-1
lim 0 = lim = 0
x 2 x-x 0 x 2 x-1
→
→
h(x)-h(2) h(x)-h(2)
lim ô lim
x 2 x-2 x 2 x-2
→
→
Συνεπώς η h δεν είναι παραγωγίσιμη στο χ 2=2
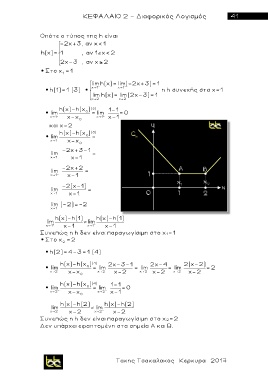
Δεν υπάρχει εφαπτομένη στα σημεία Α και Β.

Τακης Τσακαλακος Κερκυρα 2017