Page 40 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 40

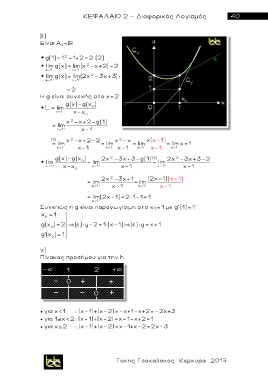
β )
Είναι A g=

g(1)=1 -1+2=2 (2)
2
lim g(x)= lim(x -x+2 ) 2
2
x 1 - x 1 -
→
→
lim g(x)= lim(2x -3x+3 )
2
x 1 + x 1 +
→
→
=2
Η g είναι συνεχής στο χ=2
L= lim g(x)-g(x )
0
x 1 - x-x
→
0
2
x -x+2-g(1)
= lim
x 1 - x-1
→
2
2
(2) x -x+2-2 x -x x(x-1)
= lim = lim = lim = lim x= 1
x 1 - x-1 x 1 - x-1 x 1 - x-1 x 1 -
→
→
→
→

g(x)-g(x ) 2x -3x+3-g(1) (2) 2x -3x+3-2
2
2
lim 0 = lim = lim
x 1 + x-x x 1 + x-1 x 1 + x-1
→
→
→
0
2x -3x+1 (2x-1)(x-1)
2
= lim = lim
-
x 1 + x-1 x 1 + x 1
→
→
-
= lim(2x-1)= 2 1 1= 1
x 1 +
→
Συνεπώς η g είναι παραγωγίσιμη στο χ 0=1 με g'(1)=1
χ 1
0
g(χ )= 2 (ε): y-2= 1×(x-1) (ε): y= x+1
0
g'(χ )= 1
0

γ)
Πίνακας προσήμου για την h

 για χ<1 : |χ-1|+|χ-2|=-χ+1-χ+2=-2χ+3
 για 1ºχ<2: |χ-1|+|χ-2|=χ-1-χ+2=1
 για χ 2 : |χ-1|+|χ-2|=χ-1+χ-2=2χ-3

Τακης Τσακαλακος Κερκυρα 2017