Page 39 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 39

ΠΑΡΑΔΕΙΓΜΑΤΑ

1.
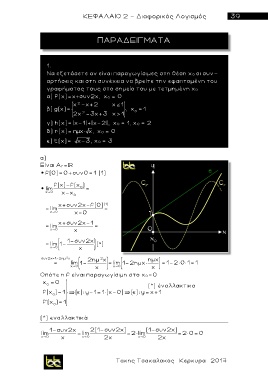
Να εξετάσετε αν είναι παραγωγίσιμες στη θέση x 0 οι συν-
αρτήσεις και στη συνέχεια να βρείτε την εφαπτομένη του
γραφήματος τους στο σημείο του με τετμημένη x 0
α) f(x)=χ+συν2χ, x 0 = 0
2
β ) g(x)= x -x+2 x 1 , x = 1
2
2x -3x+3 x> 1 0
γ) h(x)=|χ-1|+|χ-2|, x 0 = 1, x 0 = 2
δ ) r(x)= × x, x 0 = 0

ε) t(x)= x-3, x 0 = 3

α )

Είναι A f=

f(0)= 0+συν0= 1 (1)

f(x)-f(x )
lim 0 =
→
x 0 x-x 0
x+συν2x-f(0) (1)
= lim =
→
x 0 x-0

x+συν2x-1
= lim x

x 0
→
1-συν2x
= lim 1- (*)
x 0 x
→

2
συν2x = 1 - 2ημ x 2ημ x ημx
2
= lim 1- = lim 1-2ημx× = 1-2× 0× 1= 1
x 0 x x 0 x
→
→
Οπότε η f είναι παραγωγίσιμη στο χ 0=0
χ 0
0 (*) έναλλακτικα
f(χ )= 1 (ε): y-1= 1×(x-0) (ε): y= x+1
0
f'(χ )= 1
0

(*) εναλλακτικά

lim 1-συν2x lim 2(1-συν2x) 2 lim (1-συν2x) =2× 0=0
x 0→ x x 0→ 2x x 0→ 2x

Τακης Τσακαλακος Κερκυρα 2017