Page 376 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 376

3. DE L'HOSPITAL (ΑΠΡΟΣΔΙΟΡΙΣΤΙΑ 0 , 0 , 0 , 1 )
0
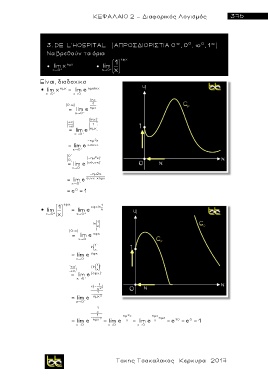
Να βρεθούν τα όρια
εφx
● lim x ημx ● lim 1
x 0 x 0 x

Είναι, διαδοχικα
lim x ημx = lim e ημx×lnx
x 0 x 0
lnx

(0 × ) 1
= lim e ημx
x 0
(lnx)'
+
+ 1 '
= lim e ημx
x 0
2
- ημ x

= lim e x×συνx
x 0
0 (- ημ x)'
2
0
= lim e (x×συνx)'
x 0
- ημ2x

= lim e συνx -xημx
x 0
= e = 1
0

lim 1 εφx = lim e εφx×ln 1 x

x 0 x x 0
1
ln
x
(0 × ) 1
= lim e εφx
x 0
1
ln
x
= lim e σφx
x 0
+ (ln 1 )'
+ x
= lim e (σφx)'
x 0
1
x×(- 2 )
x
1
- 2
= lim e ημx
x 0
1
-
x 2
1
- 2 ημ x ημx ×ημx
= lim e ημx = lim e x = lim e x = e 1×0 = e = 1
0
x 0 x 0 x 0

Τακης Τσακαλακος Κερκυρα 2017