Page 377 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 377

4. DE L'HOSPITAL (ΣΥΝΕΧΕΙΑ)
Δίνεται η συνάρτηση f με τύπο
xlnx
f(x) 1-x , x (0, 1) (1, + )

-1 , x= 1
a) Να αποδείξετε ότι η συνάρτηση f είναι συνεχής
β) Bρείιτε την εξίσωση της εφαπτομένης της C f στο ση-

μείο της Α(1, f(1))

● Πεδίο ορισμού:Α=(0, + )
● f(1)=-1
α )
xlnx
● lim f(x)= lim
x 1 x 1 1 x
0
0 (xlnx )'
= lim
x 1 (1 x )'

lnx x 1
lim x
x 1 1
lnx 1
lim 1
x 1 1

αρα η συνάρτηση f είναι συνεχής στο χ 0=1
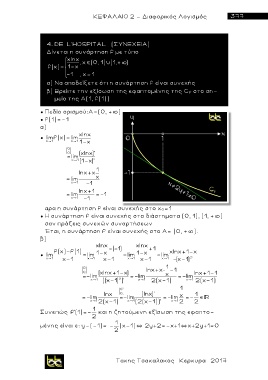
● Η συνάρτηση f είναι συνεχής στα διάστηματα (0, 1), (1, + )
σαν πράξεις συνεχών συναρτήσεων
Έτσι, η συνάρτηση f είναι συνεχής στο Α= (0, + ).
β )
xlnx ( 1 ) xlnx 1
f(x)-f(1) 1 x 1 x xlnx 1 x
● lim = lim lim lim
x 1 x 1 x 1 x 1 x 1 x 1 x 1 (x 1 ) 2

0 lnx x 1 1
0 (xlnx 1 x ) x lnx 1 1
lim lim lim
2
x 1 ((x 1 ) )' x 1 2(x-1) x 1 2(x-1)
0 1
x
lim lnx 0 lim (lnx)' lim 1
x 1 2(x-1) x 1 (2(x-1))' x 1 2 2
1
Συνεπώς f'(1)=- και η ζητούμενη εξίσωση της εφαπτο-
2
1
μένης είναι ε: y-(-1)= - (x-1)` 2y+2=-x+1`x+2y+1=0
2

Τακης Τσακαλακος Κερκυρα 2017