Page 381 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 381

2. ΑΣΥΜΠΤΩΤΕΣ (ΠΛΑΓΙΑ)
4
Δίνεται η συνάρτηση f με τύπο f(x)=χ + 2+ 2+e x
Να βρεθούν οι πλάγιες ασύμπτωτες της C f .

● Πεδίο ορισμού : Α=
● Είναι στο +
f(x)
● lim =
x +
4
x+2+
lim 2+e x
x +
2 4
= lim 1+ + 1
x
x + χ(2+e )
αφού
2
lim = 0,
x +

lim 4 0
x
x + χ(2+e )
4 4
● lim [f(x)- ]= lim x+2+ lim 2+ 2
x + x + 2+e x x + 2+e x
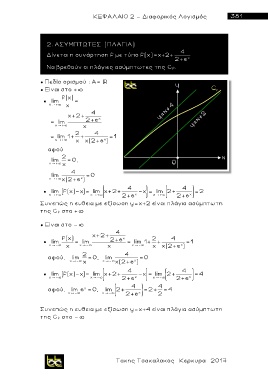
Συνεπώς η ευθεια με εξίσωση y=x+2 είναι πλάγια ασύμπτωτη

της C f στο +

● Είναι στο -

x+2+ 4
f(x) 2+e x 2 4
● lim = lim = lim 1+ + 1
x
x - x - x - χ(2+e )
αφού, lim 2 = 0, lim 4 0
x
x - x - χ(2+e )
4 4
● lim [f(x)- ]= lim x+2+ lim 2+ 4
x - x - 2+e x x - 2+e x
4 4
αφού, lim e =0, lim 2 2 4
x
x - x - 2+e x 2

Συνεπώς η ευθεια με εξίσωση y=x+4 είναι πλάγια ασύμπτωτη
της C f στο -

Τακης Τσακαλακος Κερκυρα 2017