Page 380 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 380

ΠΑΡΑΔΕΙΓΜΑΤΑ

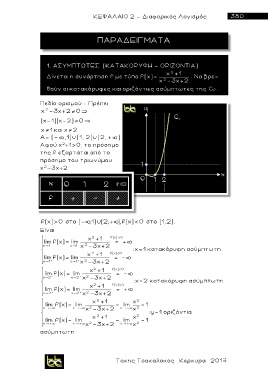
1. ΑΣΥΜΠΤΩΤΕΣ (KATAKOΡYΦH - OΡIZONTIA)
x 2 +1
Δίνεται η συνάρτηση f με τύπο f(x)= x -3x+2 . Να βρε-
2
θούν οι κατακόρυφες και οριζόντιες ασύμπτωτες της C f .

Πεδίο ορισμού : Πρέπει
x -3x+2 0
2
(x-1)(x-2) 0

x 1 και x 2
Α= (- ,1)∪(1, 2)∪(2, + )
Αφού χ +1>0, το πρόσημο
2
της f εξαρτάται από το
πρόσημο του τριωνύμου

χ -3χ+2
2

f(x)>0 στο (- ,1) (2,+ ), f(x)<0 στο (1, 2).

Είναι
2
= +
lim f(x)= lim x +1 f(x) > 0
2
x 1 - x 1 - x -3x+2 :χ=1 κατακόρυφη ασύμπτωτη
x 2 +1 f(x) < 0
lim f(x)= lim = -
2
x 1 + x 1 + x -3x+2
2
x +1 f(x) < 0
lim f(x)= lim = -
2
x 2 - x 2 - x -3x+2 :χ = 2 κατακόρυφη ασύμπτωτη
2
lim f(x)= lim x +1 f(x) > 0
= +
2
x 2 + x 2 + x -3x+2
x 2 +1 x 2
lim f(x)= lim = lim = 1
2
x - x - x -3x+2 x - x 2 :y=1 οριζόντια
x 2 +1 x 2
lim f(x)= lim lim = 1
2
x + x + x -3x+2 x + x 2
ασύμπτωτη

Τακης Τσακαλακος Κερκυρα 2017