Page 426 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 426

11. ΕΠΙΛΟΓΗΣ
Δίνονται οι συναρτήσεις f, g με τύπους
1
f(x) = 2x + lnx – ln(x + 1) και g(x) = 2x + x

A. 1) Να μελετήσετε την f ως προς την μονοτονία και να
βρείτε το όριο: lim f(x)
x +
2) Να βρείτε το σύνολο τιμών της f και το πλήθος ριζών
της εξίσωσης f(x) =0

3) Να δείξετε ότι η ευθεία y = 2x είναι π λ άγια ασύμπτωτη
της C f και να βρεθεί η θέση της C f σε σχέση με τη

πλάγια αυτή α σ ύμπτωτη για x ≥ 1

B. 1) Να μελετήσετε την g ως προς την μονοτονία και να
βρείτε το όριο: lim g(x)
x +
2) Να δείξετε ότι η C g έχει την ίδια πλάγια ασύμπτωτη με

την C f και να βρεθεί η θέση της C g και της πλάγιας

αυτής ασύμπτωτης για x ≥ 1
3) Αν h(x) = (x + 1) ln(x + 1) – x lnx , x ≥ 1 να βρείτε την
πάραγωγο της h και να βρείτε μιά αρχική συνάρτηση
της φ(x) = g(x) – f(x).

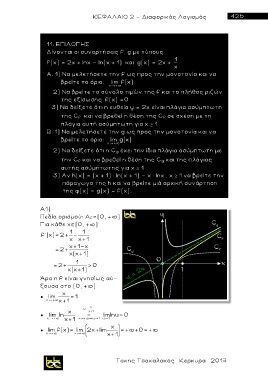
Α1)
Πεδίο ορισμού: Α f=(0, + )
Για κάθε χ (0, + )

f ΄ (x)= 2+ 1 - 1
x x+1

= 2+ x+1-x
x(x+1)

1
= 2+ > 0
x(x+1)
Άρα η f είναι γνησίως α ύ -
ξουσα στο (0, + )
x
● lim = 1
x + x+1
x
u =
x x+1
● lim ln = limlnu=0
x + x+1 x + ~ u 1 u 1
x
● lim f(x)= lim 2x+lim =+ +0=+
x + x + x+1

Τακης Τσακαλακος Κερκυρα 2017