Page 421 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 421

9. ΕΠΙΛΟΓΗΣ
α) Θεωρούμε τη συνάρτηση f : (0, + ) με
f(x) = 2x +2lnχ-1
3
1

Να αποδείξετε ότι υπάρχει μοναδικό α 2 , 1 , τέτοιο,
ώστε f(α)=0
lnx
β) Να μελετήσετε τη συνάρτηση g με τύπο g(x)=2x- x 2

ως προς τη μονοτονία και τα ακρότατα στο διάστημα
(0, + ) και να αποδείξετε ότι

α 2 g(x)+2lnα 1, για κάθε χ>0

γ) Να αποδείξετε ότι υπάρχει κ , τέτοιο, ώστε
f(κ) lnα ln(α+1)
=2+ -
κ 3 α 2 (α+1) 2

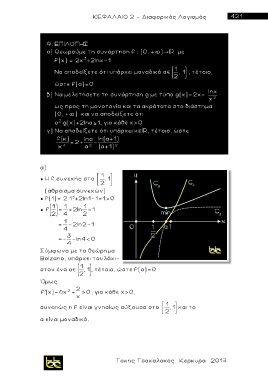
α)

1
● H f συνεχής στο , 1
2
(άθροισμα συνεχών )
● f(1)= 2 1 +2ln1-1=1>0
3
1 1 1
● f = +2ln -1
2 4 2
1
= -2ln2-1
4

=- 3 -ln4< 0
4
Σύμφωνα με το θεώρημα
Bolzano, υπάρχει τουλάχι-

1
στον ένα α , 1 , τέτοιο, ώστε f(α)=0
2
Όμως
2
f'(x)= 6x 2 + >0, για κάθε χ>0,
x
1
συνεπώς η f είναι γνησίως αύξουσα στο , 1 και το
2

α είναι μοναδικό.

Τακης Τσακαλακος Κερκυρα 2017