Page 423 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 423

10. ΕΠΙΛΟΓΗΣ
Δίνεται η συνάρτηση f με τύπο
x(e +1)
x
, x 0
f(x) = e -1
x
λ , x= 0
α) Να βρείτε το λ ώστε η f να είναι συνεχής στο
β) Να αποδείξετε ότι η f είναι παραγωγίσιμη στο
2x

γ) Να αποδείξετε ότι e - 2x e x 1 για κάθε x 0
δ) Να μελετήσετε την f ως προς τη μονοτονία

ε) Να δείξετε ότι η f στρέφει τα κοίλα άνω στο
στ) Να δείξετε ότι η f’ είναι γνησίως αύξουσα στο και ότι

το σύνολο τιμών της f’ είναι το (- 1, 1) .

α)
x
x×(e +1)
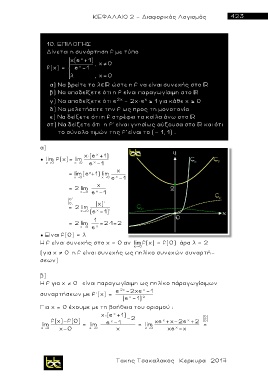
● lim f(x)= lim
x
x 0 x 0 e -1
= lim(e +1) lim x
x
x
x 0 x 0 e -1
x
= 2 lim
x
x 0 e -1
0
0 (x)'
= 2 lim
x
x 0 (e -1)'
= 2 lim 1 =2∙1=2
x 0 e x
● Είναι f(0) = λ
Η f είναι συνεχής στο x = 0 αν limf(x) = f(0) άρα λ = 2
x 0
(για x 0 η f είναι συνεχής ως πηλίκο συνεχών συναρτή-
σεων)

β )

Η f για x 0 είναι παραγωγίσιμη ως πηλίκο πάραγωγίσιμων
e 2x -2xe -1
x
συναρτήσεων με f΄(x) =
(e -1) 2
x
Για x = 0 έχουμε με τη βοήθεια του ορισμού :
x (e +1) 0
x
f(x)-f(0) e -1 -2 xe +x-2e +2 0
x
x
x
lim = lim = lim =
x
x 0 x-0 x 0 x x 0 xe -x

Τακης Τσακαλακος Κερκυρα 2017