Page 429 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 429

12. ΕΠΙΛΟΓΗΣ
Έστω οι συναρτήσεις f, g δύο φορές παραγωγίσιμες στο
με g(x) = f(x) – x 3 + 3x 2 + x + 1 για κάθε x

Επιπλέον ισχύουν :
f(-1)=-4, f(2)=-7 και f(x) x 3 -3x –x-1 για κάθε x
2

Να δείξετε ότι :
α) Υπάρχει τουλάχιστον ένα ξ (- 1, 2) τέτοιο ώστε:
f’(ξ) = 3ξ 2 - 6ξ – 1
β) g'(2) = g’ ( - 1)

γ) Υπάρχουν ξ 1 , ξ 2 (- 1, 2) τέτοια ώστε :

g''( ξ 1 ) = g''( ξ 2 ) = 0
δ) Υπάρχει τουλάχιστον ένα σημείο Μ ( n, f(n)), n (- 1, 2)

της C f , στο οποίο η f δέχεται οριζόντια εφαπτομένη.

ε) Υπάρχουν n 1 (- 1, n) και n 2 (n, 2) τέτοια ώστε
f''(n 1 ) ∙ f''(n 2 ) > 0 .

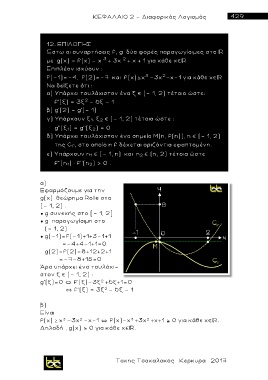
α)
Εφαρμόζουμε για την
g(x) θεώρημα Rolle στο
[- 1, 2] .
● g συνεχής στο [- 1, 2]
● g παραγωγίσιμη στο
(- 1, 2)
● g(-1)=f(-1)+1+3–1+1
=-4+4–1+1=0

g(2)=f(2)–8+12+2+1
=-7–8+15=0
Άρα υπάρχει ένα τουλάχι-
στον ξ (- 1, 2) :
g’(ξ)=0 ` f’(ξ)-3 ξ 2 +6ξ+1=0
` f’(ξ) = 3ξ 2 - 6 ξ – 1

β)
Είναι
f(x) ≥ x 3 -3x 2 –x–1 ` f(x)–x 3 +3x 2 +x+1 0 για κάθε x .
Δηλαδή , g(x) 0 για κάθε x .

Τακης Τσακαλακος Κερκυρα 2017