Page 434 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 434

14. ΕΠΙΛΟΓΗΣ
Δίνεται η συνεχής συνάρτηση f:[0, + ) , για την οποία
ισχύει: x f'(x) = x+f(x) για κάθε χ και f(1)=1
α) Να αποδείξετε ότι

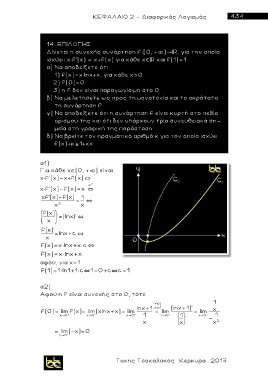
1) f(x)=x lnx+x, για κάθε χ>0
2) f(0)=0
3) η f δεν είναι παραγωγίσιμη στο 0
β) Να μελετήσετε ως προς τη μονοτονία και τα ακρότατα
τη συνάρτηση f
γ) Να αποδείξετε ότι η συνάρτηση f είναι κυρτή στο πεδίο

ορισμού της και ότι δεν υπάρχουν τρία συνευθειακά ση -
μεία στη γραφική της παράσταση
δ) Να βρείτε τον πραγματικό αριθμό κ για τον οποίο ισχύει

f(x)+κ 1+κχ

α1)
Για κάθε χ (0, + ) είναι
x f'(x)=x+f(x)`

: χ 2
x f'(x)-f(x)=x `
x f'(x)-f(x) 1 `
χ 2 x
f(x) ' (lnx )' `
χ

f(x) lnx c `
χ
f(x) χ lnx χ c `
f(x)=χ× lnx+χ

αφού, για χ=1
f(1) 1 ln1 1 c ` 1 0 c ` c 1

α2)
Αφού η f είναι συνεχής στο 0, τότε

1
lnx+1 (lnx+1)' x
f(0) = lim f(x) = lim(xlnx+x)= lim = lim lim
x 0 x 0 x 0 1 x 0 1 ' x 0 1
x x x 2

= lim(-x) = 0
x 0

Τακης Τσακαλακος Κερκυρα 2017