Page 437 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 437

15. ΕΠΙΛΟΓΗΣ
lnx
Δίνεται η συνάρτηση f με τύπο: f(x)= x , για κάθε χ>0
α) Να μελετήσετε τη συνάρτηση f ως προς τη μονοτονία

και τα ακρότατα
β) Να αποδείξετε ότι x x+ 201 7 >(x+2017) , για κάθε χ>e
x
γ) Να βρείτε το σύνολο τιμών της συνάρτησης f
δ) Να βρείτε το πλήθος των λύσεων της εξίσωσης χ= e κχ ,

χ>0 για τις διάφορες τιμές του κ

ε) Να λύσετε την εξίσωση (ημχ) συ νχ =(συνχ) ημχ στο
π
διάστημα 0,
2

στ) Να αποδείξετε ότι υπάρχει μοναδικό ξ (0, + ) ώστε η
εφαπτομένη της C f στο σημείο της Μ(ξ, f(ξ)) να τέμ-

νει τον άξονα y'y στο -1
ζ) Να αποδείξετε ότι για κάθε χ e ισχύει

2
2
f(x+1)< ln (x 1) ln x <f(x)
2
2
η) Να υπολογίσετε το όριο lim (ln (x 1 ) ln x )
2
x +

α)
Η f είναι συνεχής στο

(0, + ) (πηλίκο συνεχών)
και παραγωγίσιμη με
1-lnx
f'(x)=
χ 2
● f'(x)=0`1-lnx=0
`x=e
● f'(x)>0`1-lnx>0
`x<e
● f'(x)<0`1-lnx <0
`x>e

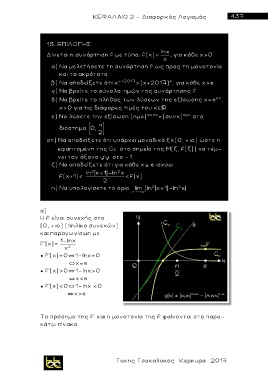
Το πρόσημο της f' και η μονοτονία της f φαίνονται στο παρα-
κάτω πίνακα

Τακης Τσακαλακος Κερκυρα 2017